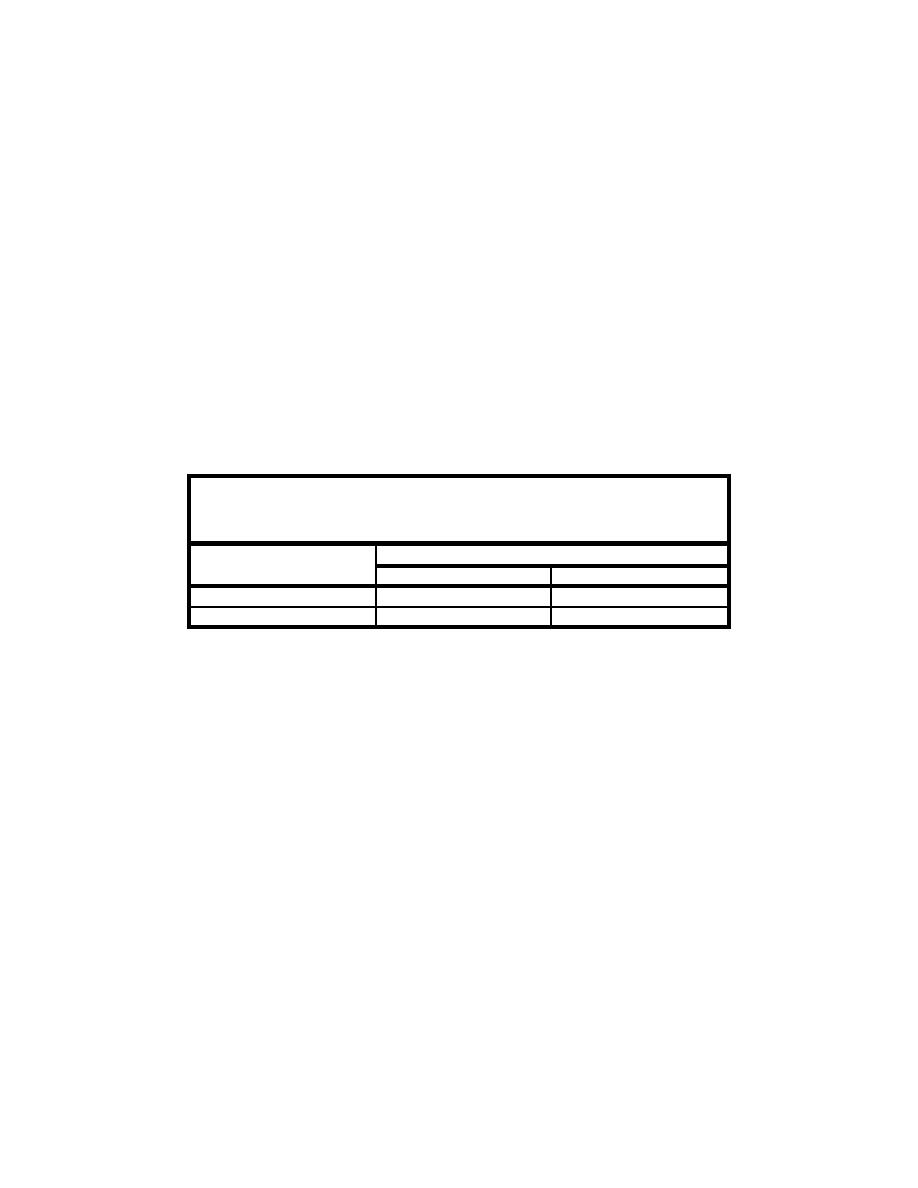
Table L-1: Types of Errors in Hypothesis Testing and Associated Probabilities

mean effect of the treatment is not less than that for the reference. Type II errors

occur when H0 is not rejected when it actually should have been rejected (e.g., in

Case 2, it is concluded that there is no difference in mean effects of the treatment

and reference when, in fact, the true mean effect of the treatment is greater than

that of the reference).

To be environmentally protective in dredged material disposal evaluations, it

is more important to guard against Type II errors. A Type II error could result in

inappropriate placement of dredged sediment, while a Type I error could result

in more costly placement alternatives. The probability of a Type I error is often

represented by the letter a ; the probability of a Type II error is often written as .

The significance level or confidence level of a statistical test is 1 - a . The power

of a test is 1 - , which is the probability of rejecting H0 when it should be

rejected, or in other words, the power to detect true significant differences. For

example, in Case 2 above, the power is the probability of concluding that the

mean effect is greater in the treatment than in the reference when, in fact, this is

true. The types of errors and their associated probabilities are summarized in

Table L-1.

Table L-1

Types of Errors in Hypothesis Testing and Associated

Probabilities

True State of Nature

Hypothesis Test Conclusion

H0 True

H0 False

H0 True(do not reject)

Correct (probability = 1 - a)

Type II Error (probability = )

H0 False(reject)

Type I Error (probability = a)

Correct (probability = 1 - )

In hypothesis testing, the Type I error rate is usually prespecified (biological

tests, by convention, generally set a = 0.05, although there is nothing magical

about this probability). An ideal statistical procedure for hypothesis testing

seeks to maintain the predetermined a , while minimizing the Type II error rate

(i.e., maximizing power). It may not be possible to do both, particularly if the

sample data depart from a normal distribution. A test that does well in

maintaining the predetermined a , regardless of the characteristics of the sample

data, is considered "robust." Tests included in this Appendix were chosen

primarily on the basis of power rather than robustness, as the consequences of

Type II error were considered more severe than those of Type I error.

Simple formulae for calculating the power of certain statistical tests used in

this Appendix are presented along with the descriptions of the tests in Sections

L.2.1.1.1, L.3.1, L.3.2.1, and L.3.2.2. The formulae may be used to calculate the

sample size required to ensure a specific power of detecting an effect of a given

magnitude (effect size), assuming that the effect exists. The formulae can also

be used to calculate the power of a specific sample size to detect a specified

difference. This latter approach is often more relevant than calculating required

sample sizes because budget or logistical constraints usually limit the number of

replicates that can be used in biological tests. This is especially true if the tests

include expensive chemical analyses such as bioaccumulation tests.

Appendix L

Statistical Methods