Figure L-5. Comparison of mean dredged material contaminant tissue levels and 95 percent upper confidence level (UCL) with hypothetical action level

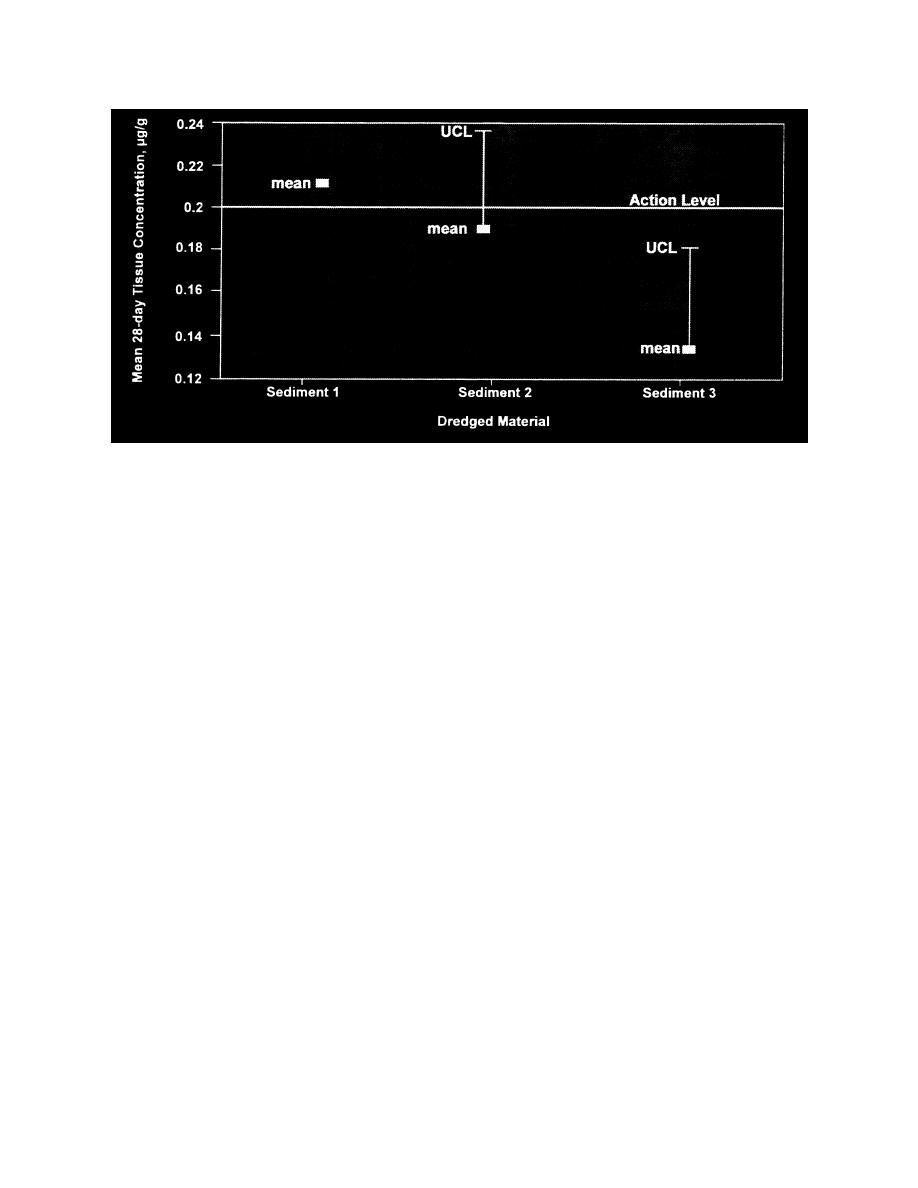Figure L-5. Comparison of mean dredged material contaminant tissue levels and 95 percent upper

confidence level (UCL) with hypothetical action level

Formulae for calculating statistical power for comparisons to a fixed

standard such as an action level are very similar to Equations L-8 and L-9:

n = ( t 1-α ,v + t 1-β ,v )2 ( s 2/ d 2 )

(L-28)

where s2 and v (degrees of freedom) are MSE and N - k if variances are equal (or

expected to be equal, if the calculation is made prior to testing), and s2 for the

individual sediment and ni - 1 if variances are unequal. It is usually easier to use

the z-approximation (from Alldredge 1987) to avoid solving for n iteratively:

n = ( z 1-α + z 1-β )2 ( s 2/ d 2 ) + 0.5( z 1-α )

(L-29)

The formulae indicate that the sample size required to detect any given

difference d will be approximately one-half that required for a comparison of

two treatments. The sample size required is lower because the comparison is

made to a fixed value, rather than to a reference which can also vary. Thus, at

least in theory, there is no sampling uncertainty or error for the fixed standard

and we know the true value of one of the two things being compared.

Using the z-approximation and s2 = MSE, the sample size required to provide

a 0.95 probability (1 - = 0.95) of detecting a tissue level 25 percent (0.05 g/g)

below the action level is:

n = (1.645 + 1.645)2(0.003763)/0.0025 + 0.5(1.645)2 = 18

(L-30)

The minimum significant difference is:

dmin = t0.95,16(MSE/n)2 = 1.746(0.003763/5)2 = 0.048 g/g

(L-31)

L38

Appendix L Selected Resource Documents